

18 is under influence of forces that are not normally present in the system. 18, lies above the upper control limit, which indicates that special causes are present in the process.
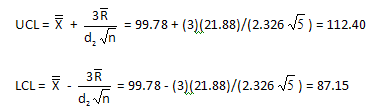
Similar to the run chart, the control charts is a line graph showing a measure (y axis) over time (x axis).
XBAR R VS XBAR S GENERATOR
However, I suggest that you avoid the chapter on run charts in this book, since it promotes the use of certain run chart rules that have been proven ineffective and even misleading (Anhoej 2015).īefore we start, we will load the qicharts package and lock the random number generator in order to make reproducible data sets for this vignette.įigure 1: I chart showing common cause variation In particular, the sections on rare events T and G control charts and the detailed explanation of prime charts are most helpful. Also, The Healthcare Data Guide (Provost 2011) is very useful and contains a wealth of information on the specific use of control charts in healthcare settings. I highly recommend Montgomery’s Introduction to Statistical Process Control (Montgomery 2009). If not, I suggest that you buy a good, old fashioned book on the subject. I assume that you are already familiar with basic control chart theory. I recommend that you read the vignette on run charts first for a detailed introduction to the most important arguments of the qic() function.
XBAR R VS XBAR S HOW TO
Dot Plot - How to create a simple dot plot in a spreadsheet without a chart object.The purpose of this vignette is to demonstrate the use of qicharts for creating control charts.Box and Whisker Plot - Create a box plot in Excel for multiple data sets.Pareto Chart - This template helps you perform a pareto analysis to analyze most significant factors.Other Templates related to Control Charts This requires the use of the Gamma function for calculating factorials of half-integer numbers (see this blog post). The hardest part of creating the s-chart is calculating the c 4 factor. This is why the X-bar chart is limited to sample sizes of 2 to 25. After trying to read through reference, I decided not to try the numerical integration of the range distribution within Excel, so I just hard-coded the values for the factors into an array.

W is commonly referred to as the relative range or studentized range and is used to estimate the process standard deviation when only the sample mean and range are known. These factors are the mean and standard deviation of the statistic W = R/ s, respectively and can be found tabulated in most text books or references about control charts. I know I'm eventually going to get asked about how the values for d 2 and d 3 are calculated for the X-bar and R charts. Reference is a great online resource that explains the formulas and steps for creating these control charts. I created these control charts based on the terminology used in reference below. The Control Chart Template above works for the most common types of control charts: the X-Bar chart (plotting the mean of a sample over time), the R chart (plotting the range or Max-Min of a sample over time), and the s chart (plotting the sample standard deviation over time). In the X-bar & S chart, n must be greater than 4. Note: In the X-bar & R control chart, the number of observations per sample (n) can be between 2 and 25. Evaluate process capability (Cp, CPU, CPL, Cpk, and % Yield) for given specification limits. Control limits are calculated based on the data you enter. This template contains a pre-made control chart for sample Mean and Range, or sample Mean and Standard Deviation (2 worksheets in one).


 0 kommentar(er)
0 kommentar(er)
